Tide Prediction
HAMELS vs. NOAA/NOS
Armed with as few as nine of the major tidal constituents (see tide analysis module), you can make a quite respectable tide prediction using the HAMELS method (Harmonic Analysis, Method of Least Squares). One model that HAMELS can use is simply the sum of nine tidal constituents symbolized as follows:
![]()
Each symbol shown above represents a cosine wave with a frequency or “speed” that uniquely identifies the tidal constituent – M2, for example, is the major lunar semidiurnal constituent with a speed of 28.984 degrees per mean solar hour. The amplitude and phase of the wave vary from place to place, however, and must be found through tide analysis. The amplitude and phase values are known as the tidal harmonic constants for the place in question.
An example of a daily tide prediction is shown below for the Chesapeake Bay Bridge Tunnel in Virginia. This prediction was made with tidal harmonic constants obtained from a recent HAMELS analysis of water level data collected by the National Oceanic and Atmospheric Administration (NOAA), National Ocean Service (NOS). Along with water level data, NOAA/NOS lists the harmonic constants from its own analysis at this station. Why not use those constants to make tide predictions?
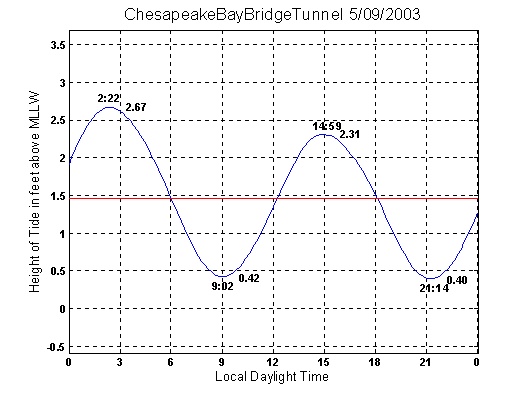
You can, but there are some things to think about first. NOS routinely applies a “buildup” factor to their tidal constituent amplitudes. The use of this factor has to do with risk management strategy; in effect it lessens the risk of under-predicting the tide (highs higher than predicted; lows lower than predicted). NOS does a similar thing with soundings on nautical charts, rounding certain fractional numbers downward so that the risk of overstating the depth of a shoal is lessened. In addition, NOS constituent phase values, or epochs, are dependent on the equilibrium tide model (see dynamic vs. static tide module). Epoch refers to the lag between the phase of the hypothetical equilibrium tide and the real (observed) tide at a given place. That means you have to calculate the phase of the equilibrium tide before you can use the NOS constants. Using the HAMELS method, phase simply refers to a particular time origin – the start of the year beginning the twentieth century, for example. Spreadsheets such as Microsoft’s Excel use this same origin in calculating serial dates and times. Lastly, NOS does not list the date of the analysis used to determine the tidal harmonic constants published on their web site, http://co-ops.nos.noaa.gov/. In some instances, the tidal harmonic constants are considerably older than the water level data available for downloading.
If NOS harmonic constants are sometimes difficult to use, the tidal datum elevations available at most NOS tide stations are very simple and straightforward. They come in handy when you want your tidal predictions to refer to a specific datum such as Mean Lower Low Water (MLLW). Tidal height predictions initially refer to the base elevation in the absence of a tide – Mean Sea Level (MSL). If you want them to refer to MLLW instead, add the amount of offset (MSL-MLLW) between the two datums to the tide model.
NOS normally use thirty-eight tidal constituents in their official predictions at stations in North and South America, part of a broader effort consistent with their legal responsibilities for vessel navigation and marine safety. The additional constituents can improve the final prediction of, say, the time and height of a certain high tide by a few minutes or a few centimeters – but generally no more than that. The lion’s share of the difference between a prediction and an observation of a given tide, as tide analysis repeatedly shows, rests with the so-called meteorological tide caused by winds and barometric pressure changes. A purely astronomical tide model is incapable of accounting for this part of the daily change in water level but hydrodynamic models using data assimilation techniques are beginning to fill the void.
While a HAMELS analysis by definition fits each water level data set with the least error possible for a given mix of tidal constituents, the question remains - how well does it agree with a different, or independent, data set? Verification of the harmonic model is still somewhat subjective (how well is well enough?) but employing independent plots such as the following provide a partial answer to this question. As often happens in January, a northeaster occurred in lower Chesapeake Bay on the first day of 2003, causing observed water levels to rise well above predicted levels at the Chesapeake Bay Bridge Tunnel lying at the entrance to the bay. Although the water levels are different, the phase of the observed and predicted tides remain in close agreement throughout the weather event.
Chesapeake Bay Bridge Tunnel
Meters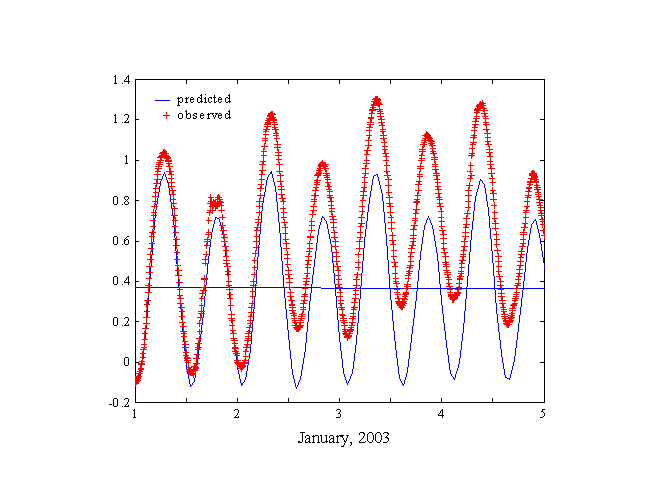
(the blue horizontal line represents MLLW)

