The Equilibrium Theory of Tides
This is sometimes called the theory of “static” tides, a theory that emerged for the first time in Isaac Newton’s famed Principia. Having identified the tide-producing forces, Newton, and others who followed him, conceived of a hypothetical global ocean in static equilibrium with these forces – an equilibrium calling for a prolate spheroid of water covering the earth. “Prolate” means that the sphere in question has been stretched along a line joining two poles; not the geographic poles in this case but the poles in line with the celestial body (moon or sun) causing the hypothetical ocean sphere to deform. Taking another look at the graphic illustrating the tractive forces in the previous module, one can easily imagine water converging on these poles to produce twin “tidal bulges” – terms that are still very popular in modern day textbooks.
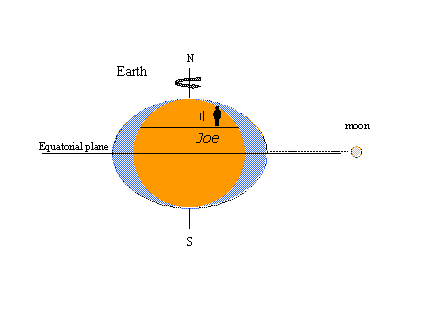
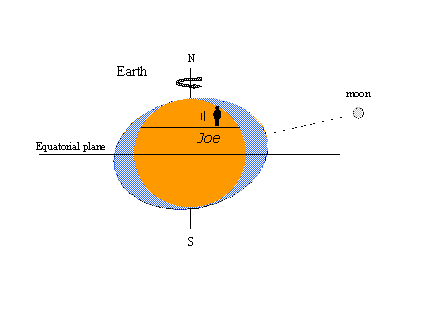
The reason for the popularity of the equilibrium theory - the tidal bulges concept at least – is that it’s easy to explain certain well-known tidal phenomena with pictures. In the one on the left below, an imaginary observer named Joe rotates with the earth and encounters the static bulges in the form of high tides. Whenever the moon crosses Joe’s local meridian, he witnesses high tide. It’s high tide again twelve lunar hours later when the moon crosses the opposite meridian on the other side of the earth. Two highs and two lows occur in one lunar day lasting 24 hours and 50 minutes in watch (solar) time. In the figure on the right, the moon has progressed in its orbit around the earth to a position north of the equator (north declination). The static bulges move to remain in line with the moon and now Joe encounters a diurnal inequality in the high tides (successive high tides of unequal height). Maximum lunar declination, north or south of the equator, produces tropic tides; tides occurring when the moon is on the equator are called equatorial tides. Tropic-equatorial tides recur twice in an interval of 27 1/3 days – the tropic month covering one complete cycle in lunar declination. All these observations are consistent with equilibrium theory.
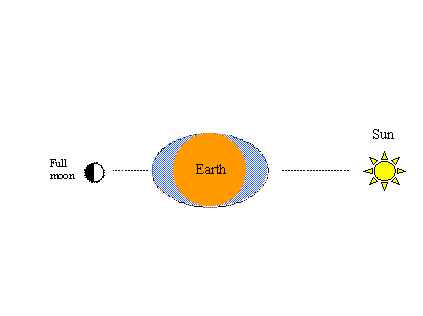
Another phenomenon that’s easy to demonstrate in this way is the well-known spring-neap cycle. Solar gravity also produces a pair of tidal bulges in the hypothetical ocean. When the tractive forces of the sun and moon are in line, spring tides of greater range (higher highs and lower lows) result as shown in the figure on the left below. As in the previous figures, when the moon completes another half-cycle in its orbit – this time from full to new moon - spring tides will occur again.
The figure below on the right illustrates the neap portion of the spring-neap cycle; i.e., when the moon is in the first quarter (or the third quarter) of that cycle, lunar and solar tractive forces are completely out-of-line, tending to counteract one another, and neap tides of lesser range (lower highs and higher lows) result. Two spring-neap cycles (two springs and two neaps) are completed in 29 ½ days, the same period of time required for the moon to complete one full orbit of earth with respect to the sun.
Other aspects of the observed tide in accordance with equilibrium theory include the perigean-apogean cycle. This one stems from the fact that the moon’s orbit around the earth describes an ellipse rather than a circle. Perigean tides of greater range occur at lunar perigee, when the moon is closest to the earth, and apogean tides of lesser range occur at lunar apogee, when the moon is farthest from the earth in its elliptical orbit. The perigean-apogean cycle takes about 27 ½ days to complete.

Although the equilibrium theory does an excellent job of explaining cyclical tidal phenomena and the recurrence periods associated with many of them, it’s an example of a model of ideal behavior – something that works for the purpose intended although it may not adhere to the truth in all instances. We don’t have far to look for those instances. The earth is only partially covered by its waters, land masses prevent anything resembling a bulge from traveling completely around it, and observations of real tides show that they do not respond instantly to the tide-producing forces of the moon and sun as the theory requires.

