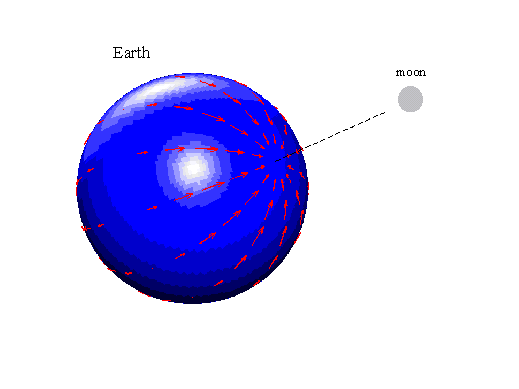
Tide-Producing Forces
Ocean tides are the result of gravitational interactions between the earth, moon, and sun and the waters of the earth. Earth’s gravity holds you and me and everything else on the earth’s surface in a firm grip. Although it’s a very small force, lunar gravity also acts on you and me and the earth itself. The reason we don’t “fall” straight into the moon is that there is a separate force counteracting the lunar attractive force.
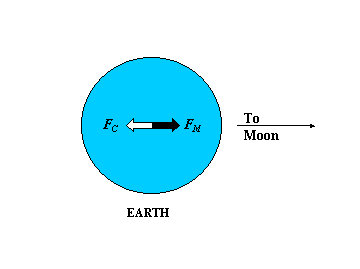 In the diagram at left, the lunar force is designated FM and the
offsetting force is the centrifugal force, FC, produced by the revolution of the earth
about its common center of gravity with the moon. If the earth and moon were
“twin planets” with equal size and mass, the common center would be a point
halfway between them but because the earth is much larger and more massive than
the moon, it’s actually a point lying just inside the earth.
In the diagram at left, the lunar force is designated FM and the
offsetting force is the centrifugal force, FC, produced by the revolution of the earth
about its common center of gravity with the moon. If the earth and moon were
“twin planets” with equal size and mass, the common center would be a point
halfway between them but because the earth is much larger and more massive than
the moon, it’s actually a point lying just inside the earth.
As the image at left shows, we can regard the forces FM and FC to be in balance (FM = FC) for the earth as a whole and acting at a single point at the earth’s center. Similarly, as the earth orbits the sun it experiences solar attractive forces like those of the earth-moon system but of lesser magnitude.
Away from the earth’s center, the forces shown above are not in balance. Local differences in the magnitude and direction of FM and FC make up the “differential” or tide producing forces that vary across the earth’s surface. The centrifugal force, FC , is the same everywhere. However, the attractive force, FM , varies inversely as the square of the distance from the moon and always points toward the center of the moon. A person standing on the earth at the point closest to the moon would experience (but hardly feel!) a differential force of about 0.0000001g per unit of mass, acting toward the moon (FM >FC), compared with the normal 1g caused by earth’s gravity alone (force = mass times acceleration; ‘g’ is the acceleration of earth’s gravity, about 32 ft/sec per sec or 9.8 m/sec per sec).
One earth diameter farther away on the opposite side of the earth from the moon, the differential force is about 0.0000001g per unit of mass, acting away from the moon (FC >FM). How can forces so small move huge volumes of water around and produce global tides? The answer lies in the amount of mass and the force direction. Vertical forces in particular are insignificant in comparison to earth’s gravity. Imagine trying to lift a small car off the ground - earth’s gravity proves more than a match for most of us and it’s even hard to push one slightly uphill! But on a level roadway, it becomes a much easier task, particularly if several friends (more mass) are helping to push. So, too, will the ocean volumes (lots of mass) respond readily to the horizontal component of the differential force - the tractive forces shown in red in the diagram below. We can think of these as a net of forces – a force field – thrown over the globe and aligned with the moon, trapping a spinning earth inside.