Are Tides Waves?
Yes and it’s essential to make that point before we can understand how tides, and tidal currents, behave in coastal environments – the place where most coastal residents are likely to encounter them. By the way, the “tide waves” discussed here are in no way related to “tidal waves” or tsunamis, the comparatively rare and very destructive seismic sea waves generated by undersea earthquakes and volcanism. Tide waves have an entirely different origin and are truly everyday events. The characteristic that easily sets them apart from wind waves and other common wave examples is their wavelength spanning thousands of nautical miles in the open ocean, giving them the name long waves. But they have other properties that identify them as well. We’ll start with the basic form of a wave as specified by its height and length.
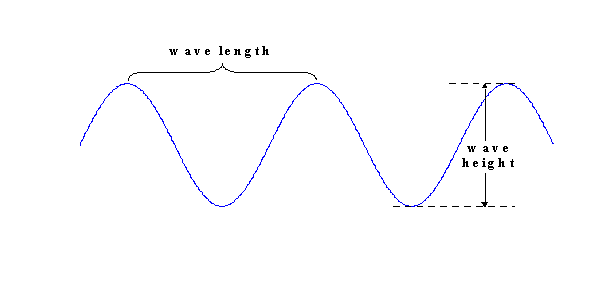
The ratio of wave height to wavelength gives the wave steepness. Obviously tide waves are pretty darn flat since their wavelengths are never less than a hundred kilometers (a kilometer is a little more than half a nautical mile) and their heights are often less than a meter. That’s why, to an observer, tides just seem to rise and fall like water in a tub without much else to suggest a moving wave. In terms of wave dynamics and what goes on inside a wave, we must compare the dimensions of the wave to the dimensions of the sea that contains them, starting with the depth. Water depth determines whether we have a deepwater wave or a shallow water wave.
Deepwater waves – As a rule, when the water depth is greater than one-half of the wavelength, the wave is classified as a deepwater wave. Water particles inside this type of wave move forward and back, up and down in a circular orbit whose diameter decreases with depth until it essentially disappears at the wave base. With each orbit, the particles inch their way forward by a slight amount producing what is called Stokes drift. The waveform itself moves forward in the direction of wave advance at a much faster rate.
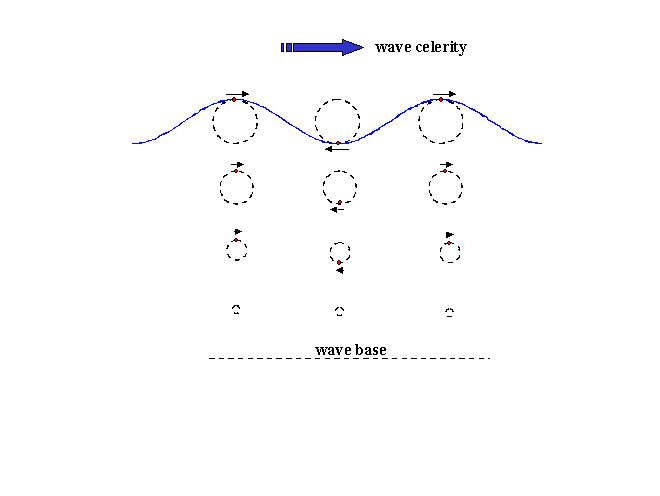
Wave celerity - The speed at which an individual wave advances or “propagates” is known as the wave celerity. For a deepwater wave the celerity is directly proportional to the wave period, T. The formula for deepwater celerity, Co, is Co =1.56T m/sec = 5.12T ft/sec. Note that the deepwater wave celerity does not depend on water depth.
Shallow
water waves - Waves are said to be in shallow water when the depth is less
than one twenty-fifth of their wavelength. After reaching this depth, the water
particle orbits inside the wave become elliptical rather than circular as the
“up-down” component of the motion is “squeezed” by the presence of the bottom.
The squeezing happens more quickly than the reduction of orbit size with depth
so that a “forward-back” motion extends all the way to the bottom. The celerity
of an individual shallow water wave, C, is given by the formula ![]() where h is
depth and g is the acceleration of gravity. Thus, the shallow water
celerity depends on depth rather than wave period.
where h is
depth and g is the acceleration of gravity. Thus, the shallow water
celerity depends on depth rather than wave period.
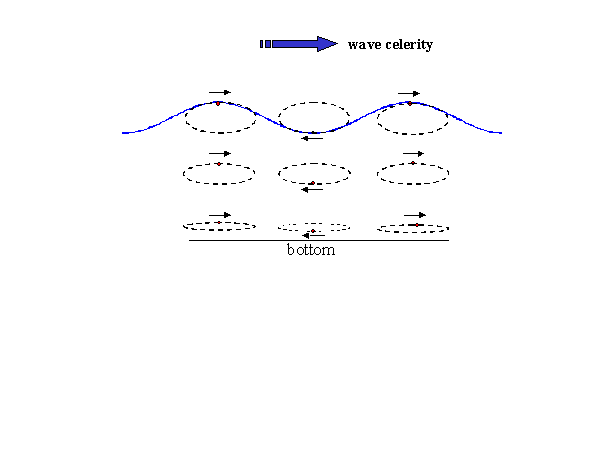
Long
waves (tides) – From the information given above, tide waves are clearly
shallow water waves the world over. A little arithmetic shows why. By
definition, the wave celerity is equal to wavelength divided by wave period; i.e.,
C=L/T. Thus, for a shallow water wave, ![]() . The dominant period of the semidiurnal (twice daily) tide
being 12.42 hours and the greatest ocean depths being about 12,000 meters, the
corresponding tidal wavelength would be 15,330 km. One twenty-fifth of this is
613 km or 613,000 meters. In other words, tide waves are way too long to even
approach the limit where they would not be classified as shallow water
waves. In fact, their length-to-depth ratio is so extreme that the vertical
(“up-down”) motion of the water particles is insignificant compared to their
horizontal (“forward-back”) motion as shown below. The horizontal motion on the
other hand is quite significant as it represents the tidal current.
. The dominant period of the semidiurnal (twice daily) tide
being 12.42 hours and the greatest ocean depths being about 12,000 meters, the
corresponding tidal wavelength would be 15,330 km. One twenty-fifth of this is
613 km or 613,000 meters. In other words, tide waves are way too long to even
approach the limit where they would not be classified as shallow water
waves. In fact, their length-to-depth ratio is so extreme that the vertical
(“up-down”) motion of the water particles is insignificant compared to their
horizontal (“forward-back”) motion as shown below. The horizontal motion on the
other hand is quite significant as it represents the tidal current.
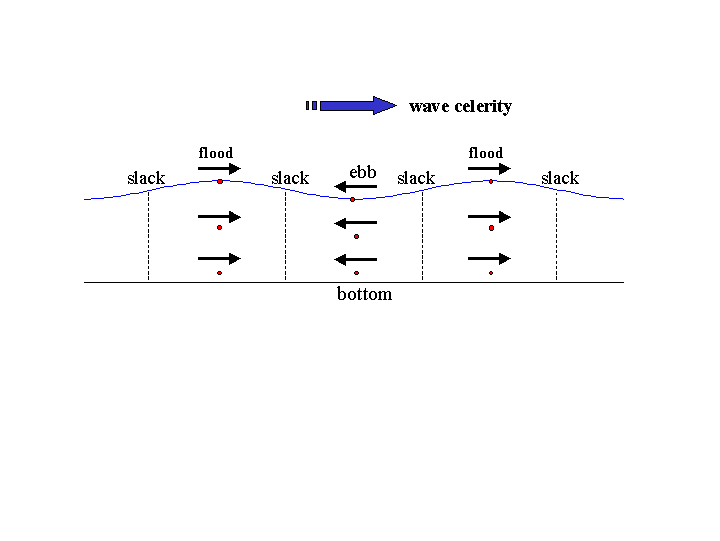
More on tidal currents - The combination of long wavelength and long period in a tide wave insures that the tidal currents induced by these waves are large-scale features as well. Assuming the durations of flood and ebb are half a lunar tidal cycle (6.21 hours) each and that the average current in either phase is half a knot (one knot is a water speed of one nautical mile per hour), then the excursion of the water masses in motion turns out to be a little more than three nautical miles in each direction. Tidal currents, in other words, operate on a scale where the Coriolis acceleration becomes important (see Dynamic Tides module). As a result, tidal currents in the open ocean usually occur in the form of rotary currents – tidal currents that flow continually with the direction of flow changing through all headings (0-360°) during a tidal cycle. However, in river estuaries with narrow confining channels, tidal currents tend to become bi-directional as the above diagram suggests.

